Binary search

Posted on Edited on In , Views:

Intro

Binary Search splits the search space into two halves and only keep the half that has the search target and throw away the other half that would not have the target. In each step, the search space is reduced to half, until the target is found. Binary Search reduces the search time from linear O(n) to logarithmic O(log n).

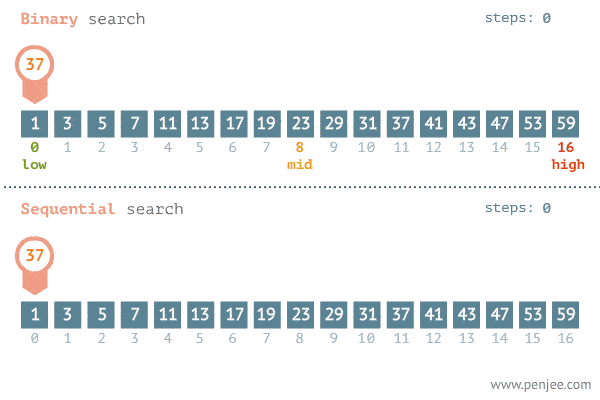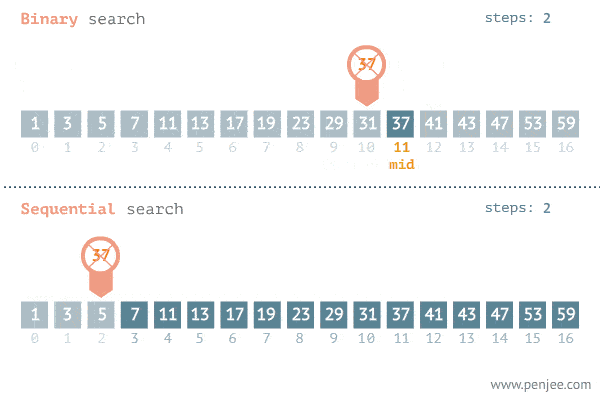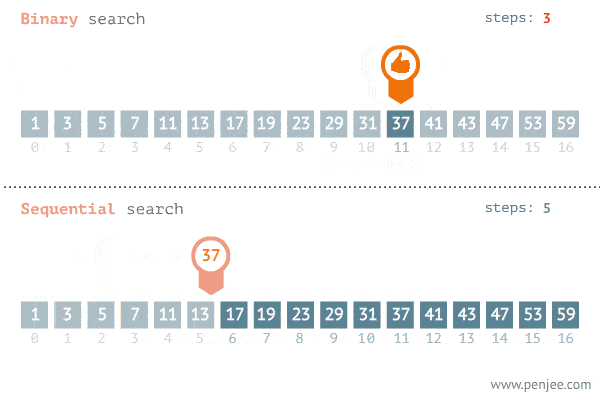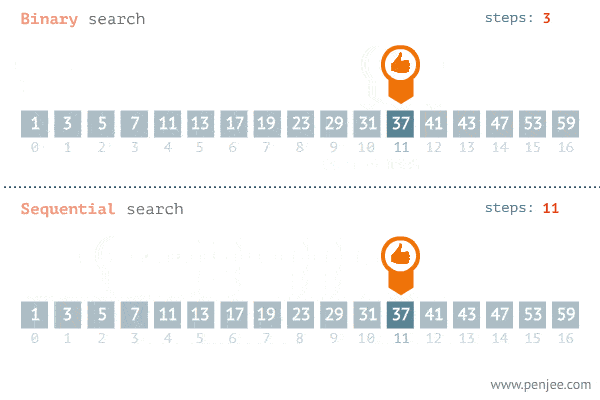
Generalized binary search template

For an array(not only for numbers) sorted in ascending order, the following is the generalized binary search template to solve many problems.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def binary_search(array) -> int:
    array.sort()

    def condition(value) -> bool: # the condition should be satisfied to get the result
        pass

    left, right = 0, len(array)  # search space
    while left < right:
        mid = left + (right - left) // 2 # try to avoid overflow
        if condition(mid): 
            right = mid
        else:
            left = mid + 1

    return left # return value could be left or left-1

Note:

  • The left and right are the boundary to include all possible elements(aka search space)
  • Is return value left or left - 1? Remember this: after exiting the while loop, left is the minimal k​ satisfying the condition function
  • Design the condition function. Let’s get more sense with the following practices.

Thanks to zhijun_liao who wrote this useful binary search article.

Basic application

[Leetcode 35] Search Insert Position

Given a sorted array of distinct integers and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.

You must write an algorithm with O(log n) runtime complexity.

Example 1:

1
2
Input: nums = [1,3,5,6], target = 5
Output: 2

Example 2:

1
2
Input: nums = [1,3,5,6], target = 2
Output: 1

Example 3:

1
2
Input: nums = [1,3,5,6], target = 7
Output: 4

Constraints:

  • 1 <= nums.length <= 104
  • -104 <= nums[i] <= 104
  • nums contains distinct values sorted in ascending order.
  • -104 <= target <= 104

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        # Note that the target element can be larger than all the elementes in nums and it would be inserted to the end
        left, right = 0, len(nums)

        while left < right:
            mid = left + (right - left) // 2
            # looking for the minimal k value satisfying nums[k] >= target
            if nums[mid] >= target:
                right = mid
            else:
                left = mid + 1

        return left

[Leetcode 69] Sqrt(x)

Given a non-negative integer x, return the square root of x rounded down to the nearest integer. The returned integer should be non-negative as well.

You must not use any built-in exponent function or operator.

For example, do not use pow(x, 0.5) in c++ or x ** 0.5 in python.

Example 1:

1
2
3
Input: x = 4
Output: 2
Explanation: The square root of 4 is 2, so we return 2.

Example 2:

1
2
3
Input: x = 8
Output: 2
Explanation: The square root of 8 is 2.82842..., and since we round it down to the nearest integer, 2 is returned.

Constraints:

  • 0 <= x <= 231 - 1

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def mySqrt(self, x: int) -> int:
        if x <= 1:
            return x
        
        left, right = 0, x
        while left < right:
            mid = left + (right - left )// 2
            if mid * mid <= x:
                left = mid + 1
            else:
                right = mid
                
        return left - 1

[Leetcode 278] First Bad Version

You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.

Suppose you have n versions [1, 2, …, n] and you want to find out the first bad one, which causes all the following ones to be bad.

You are given an API bool isBadVersion(version) which returns whether version is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.

Example 1:

1
2
3
4
5
6
7
Input: n = 5, bad = 4
Output: 4
Explanation:
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.

Example 2:

1
2
Input: n = 1, bad = 1
Output: 1

Constraints:

  • 1 <= bad <= n <= 231 - 1

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def firstBadVersion(self, n: int) -> int:
        # search boundary: [1,n]
        left, right = 1, n

        # exit condition: left == right
        while left < right:
            # reduce possibility of overflow
            mid = left + (right - left) // 2

            # condition function: isBadVersion()
            if isBadVersion(mid):
                # include mid in the next round of search since it could be the first bad version
                right = mid
            else:
                # exclude mid from the next round of search since it's NOT bad version
                left = mid + 1

        # left is the minimum value to satisfy condition function
        return left

Advanced application

[Leetcode 668] Kth Smallest Number in Multiplication Table

Nearly everyone has used the Multiplication Table. The multiplication table of size m x n is an integer matrix mat where mat[i][j] == i * j (1-indexed).

Given three integers m, n, and k, return the kth smallest element in the m x n multiplication table.

Example :

1
2
3
4
5
6
7
8
9
Input: m = 3, n = 3, k = 5
Output: 3
Explanation: 
The Multiplication Table:
1	2	3
2	4	6
3	6	9

The 5-th smallest number is 3 (1, 2, 2, 3, 3).

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution:
    def findKthNumber(self, m: int, n: int, k: int) -> int:
        # Given an input num, determine if there're at least k values <= num.
        def hasKValuesAtLeast(num) -> bool:
            # total numbers <= k
            count = 0
            # count row by row
            for row in range(1, m + 1):
                # each row has i numbers which are <= num
                i = min(num // row, n)
                # exit early if no number <= num
                if i == 0:
                    break
                # accumulate the numbers count
                count += i

            # check if there are at least k numbers <= given num
            return count >= k

        # search range is [1,m*n]
        left, right = 1, m * n
        while left < right:
            mid = left + (right - left) // 2
            # look for the minimum number satisfying hasKValuesAtLeast function
            if hasKValuesAtLeast(mid):
                right = mid
            else:
                left = mid + 1

        # the smallest number which has at least k number smaller than or equal to it
        return left

[Leetcode 719] Find K-th Smallest Pair Distance

The distance of a pair of integers a and b is defined as the absolute difference between a and b.

Given an integer array nums and an integer k, return the kth smallest distance among all the pairs nums[i] and nums[j] where 0 <= i < j < nums.length.

Example 1:

1
2
3
4
5
6
7
Input: nums = [1,3,1], k = 1
Output: 0
Explanation: Here are all the pairs:
(1,3) -> 2
(1,1) -> 0
(3,1) -> 2
Then the 1st smallest distance pair is (1,1), and its distance is 0.

Example 2:

1
2
Input: nums = [1,1,1], k = 2
Output: 0

Example 3:

1
2
Input: nums = [1,6,1], k = 3
Output: 5

Constraints:

  • n == nums.length
  • 2 <= n <= 104
  • 0 <= nums[i] <= 106
  • 1 <= k <= n * (n - 1) / 2

Solution:

Brute force with priority queue:

1
2
3
4
5
6
7
8
9
10
11
12
13
def smallestDistancePair_time_limit_exceeded(self, nums: List[int], k: int) -> int:
    minHeap = []
    heapq.heapify(minHeap)
    for i in range(len(nums)):
        for j in range(i+1, len(nums)):
            d = abs(nums[i] - nums[j])
            heapq.heappush(minHeap, d)

    kth = None
    for i in range(k):
        kth = heapq.heappop(minHeap)

    return kth

Binary search:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution:
    def smallestDistancePair(self, nums: List[int], k: int) -> int:
        nums.sort()
        n = len(nums)

        def hasKPairsAtleast(distance):
            i, j, count = 0, 0, 0
            while i < n or j < n:
                # if the distance for nums[i] and nums[j] is less than the given distance, the distance between nums[i] and nums[k](i<k<j) is also less than distance
                while j < n and nums[j] - nums[i] <= distance:
                    # extend the range
                    j += 1
                # count valid pairs:
                # [nums[i],nums[i+1]], [nums[i],nums[i+2]],..., [nums[i],nums[j-1]]
                count += j - i - 1

                # modify the start index for the range
                i += 1

            return count >= k

        # search range is [0, nums[-1]-nums[0]]
        left, right = 0, nums[-1] - nums[0]

        while left < right:
            mid = left + (right - left) // 2
            if hasKPairsAtleast(mid):
                right = mid
            else:
                left = mid + 1

        return left

[Leetcode 875] Koko Eating Bananas

Koko loves to eat bananas. There are n piles of bananas, the ith pile has piles[i] bananas. The guards have gone and will come back in h hours.

Koko can decide her bananas-per-hour eating speed of k. Each hour, she chooses some pile of bananas and eats k bananas from that pile. If the pile has less than k bananas, she eats all of them instead and will not eat any more bananas during this hour.

Koko likes to eat slowly but still wants to finish eating all the bananas before the guards return.

Return the minimum integer k such that she can eat all the bananas within h hours.

Example 1:

1
2
Input: piles = [3,6,7,11], h = 8
Output: 4

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution:
    def minEatingSpeed(self, piles: List[int], h: int) -> int:
        # check if it can finish eating with the given speed
        def canEatBananasInSpeed(speed):
            hours = 0
            for pile in piles:
                if pile % speed:
                    hours += pile // speed + 1
                else:
                    hours += pile // speed

            return hours <= h

        # search space is [1,max(piles)]
        left, right = 1, max(piles)
        while left < right:
            mid = left + (right - left) // 2
            # continue to search slower speed if it can finish eating in the speed of "mid"
            if canEatBananasInSpeed(mid):
                right = mid
            # it has to speed up since it can't finish eating in the speed of "mid"
            else:
                left = mid + 1

        # this will be slowest speed it can finish eating all bananas
        return left

[Leetcode 1011] Capacity To Ship Packages Within D Days

A conveyor belt has packages that must be shipped from one port to another within days days.

The ith package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.

Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within days days.

Example 1:

1
2
3
4
5
6
7
8
9
10
Input: weights = [1,2,3,4,5,6,7,8,9,10], days = 5
Output: 15
Explanation: A ship capacity of 15 is the minimum to ship all the packages in 5 days like this:
1st day: 1, 2, 3, 4, 5
2nd day: 6, 7
3rd day: 8
4th day: 9
5th day: 10

Note that the cargo must be shipped in the order given, so using a ship of capacity 14 and splitting the packages into parts like (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) is not allowed.

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution:
    def shipWithinDays(self, weights: List[int], days: int) -> int:
        # check if the pacages can be shipped with given capacity in days
        def canShipPackages(capacity):
            currentDayWeight = 0  # the weight has been shipped in current day
            countDays = 1  # the number of days has been spent
            for weight in weights:
                currentDayWeight += weight
                # we need to wait for the next day due to out of capacity
                if currentDayWeight > capacity:
                    currentDayWeight = weight  # reset
                    countDays += 1  # add days by 1
                    if countDays > days:
                        return False

            return True

        # the minimum capacity must be in the range of [max(weights), sum(weights)]
        left, right = max(weights), sum(weights)
        while left < right:
            mid = left + (right - left) // 2
            # packages can be shipped with capacity "mid" and we continue to search smaller capacity
            if canShipPackages(mid):
                right = mid
            # packages can not be shipped with capacity "mid" and we have to try bigger capacity which is mid+1
            else:
                left = mid + 1

        return left

[Leetcode 1201] Ugly Number III

An ugly number is a positive integer that is divisible by a, b, or c.

Given four integers n, a, b, and c, return the nth ugly number.

Example 1:

1
2
3
Input: n = 3, a = 2, b = 3, c = 5
Output: 4
Explanation: The ugly numbers are 2, 3, 4, 5, 6, 8, 9, 10... The 3rd is 4.

Example 2:

1
2
3
Input: n = 4, a = 2, b = 3, c = 4
Output: 6
Explanation: The ugly numbers are 2, 3, 4, 6, 8, 9, 10, 12... The 4th is 6.

Example 3:

1
2
3
Input: n = 5, a = 2, b = 11, c = 13
Output: 10
Explanation: The ugly numbers are 2, 4, 6, 8, 10, 11, 12, 13... The 5th is 10.

Constraints:

  • 1 <= n, a, b, c <= 10^9
  • 1 <= a * b * c <= 10^18
  • It is guaranteed that the result will be in range [1, 2 * 10^9].

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import math

class Solution:
    def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:
        ab = a * b // math.gcd(a, b)
        bc = b * c // math.gcd(b, c)
        ac = a * c // math.gcd(a, c)
        abc = a * bc // math.gcd(a, bc)

        # check if there are at least n ugly numbers <= num 
        def hasNUglyNumbersAtLeast(num):
            uglyNums = num // a + num // b + num // c - \
                num // ab - num // ac - num // bc + num // abc
            return uglyNums >= n

        left, right = 1, 10**10
        while left < right:
            mid = left + (right - left) // 2
            if hasNUglyNumbersAtLeast(mid):
                right = mid
            else:
                left = mid + 1

        return left

[Leetcode 1283] Find the Smallest Divisor Given a Threshold

Given an array of integers nums and an integer threshold, we will choose a positive integer divisor, divide all the array by it, and sum the division’s result. Find the smallest divisor such that the result mentioned above is less than or equal to threshold.

Each result of the division is rounded to the nearest integer greater than or equal to that element. (For example: 7/3 = 3 and 10/2 = 5).

The test cases are generated so that there will be an answer.

Example 1:

1
2
3
4
Input: nums = [1,2,5,9], threshold = 6
Output: 5
Explanation: We can get a sum to 17 (1+2+5+9) if the divisor is 1. 
If the divisor is 4 we can get a sum of 7 (1+1+2+3) and if the divisor is 5 the sum will be 5 (1+1+1+2).

Example 2:

1
2
Input: nums = [44,22,33,11,1], threshold = 5
Output: 44

Constraints:

  • 1 <= nums.length <= 5 * 10^4
  • 1 <= nums[i] <= 10^6
  • nums.length <= threshold <= 10^6

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def smallestDivisor(self, nums: List[int], threshold: int) -> int:
        def condition(divisor):
            s = 0
            for num in nums:
                if num % divisor:
                    s += num // divisor + 1
                else:
                    s += num // divisor

            return s <= threshold

        left, right = 1, max(nums)
        while left < right:
            mid = left + (right - left) // 2
            if condition(mid):
                right = mid
            else:
                left = mid + 1

        return left

More practices

[Leetcode 162] Find Peak Element

A peak element is an element that is strictly greater than its neighbors.

Given a 0-indexed integer array nums, find a peak element, and return its index. If the array contains multiple peaks, return the index to any of the peaks.

You may imagine that nums[-1] = nums[n] = -∞. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.

You must write an algorithm that runs in O(log n) time.

Example 1:

1
2
3
Input: nums = [1,2,3,1]
Output: 2
Explanation: 3 is a peak element and your function should return the index number 2.

Example 2:

1
2
3
Input: nums = [1,2,1,3,5,6,4]
Output: 5
Explanation: Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.

Constraints:

  • 1 <= nums.length <= 1000
  • -2^31 <= nums[i] <= 2^31 - 1
  • nums[i] != nums[i + 1] for all valid i.

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution:
    def findPeakElement(self, nums: List[int]) -> int:
        # one element
        if len(nums) == 1:
            return 0

        # check if first element is greater than second
        if nums[0] > nums[1]:
            return 0

        # check if last element is greater than second last
        if nums[-1] > nums[-2]:
            return len(nums) - 1

        # search peak in the middle
        l = 1
        r = len(nums) - 2
        while l <= r:
            mid = l + (r-l)//2
            if nums[mid] > nums[mid-1] and nums[mid] > nums[mid+1]:
                return mid
            elif nums[mid] < nums[mid + 1]:
                # nums[mid] is in ascending trend and the peak must be on the right
                l = mid + 1
            else:
                # nums[mid] is in descending trend and the peak must be on the left
                r = mid - 1

        # no peak
        return -1

[Leetcode 2300] Successful Pairs of Spells and Potions

You are given two positive integer arrays spells and potions, of length n and m respectively, where spells[i] represents the strength of the ith spell and potions[j] represents the strength of the jth potion.

You are also given an integer success. A spell and potion pair is considered successful if the product of their strengths is at least success.

Return an integer array pairs of length n where pairs[i] is the number of potions that will form a successful pair with the ith spell.

Example 1:

1
2
3
4
5
6
7
Input: spells = [5,1,3], potions = [1,2,3,4,5], success = 7
Output: [4,0,3]
Explanation:
- 0th spell: 5 * [1,2,3,4,5] = [5,10,15,20,25]. 4 pairs are successful.
- 1st spell: 1 * [1,2,3,4,5] = [1,2,3,4,5]. 0 pairs are successful.
- 2nd spell: 3 * [1,2,3,4,5] = [3,6,9,12,15]. 3 pairs are successful.
Thus, [4,0,3] is returned.

Constraints:

  • n == spells.length
  • m == potions.length
  • 1 <= n, m <= 105
  • 1 <= spells[i], potions[i] <= 105
  • 1 <= success <= 1010

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution:
    # Notice that if a spell and potion pair is successful, then the spell and all stronger potions will be successful too.
    def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:
        potions.sort()
        m = len(potions)
        res = []
        for spell in spells:
            target = success // spell
            if success % spell:
                target += 1

            insertIdx = bisect.bisect_left(potions, target)
            res.append(m - insertIdx)
        
        return res

Reference